Introduction

Knots and links are common occurrences in our daily lives, whether it's tying shoelaces or securing a package. However, beyond these practical uses, knots and links take on a more abstract yet profound form in the realm of topology, where they are studied as mathematical objects with intriguing properties. These objects play a vital role in a variety of scientific fields, particularly in understanding complex systems in physics. In this work, we focus on developing an algorithm to distinguish two fundamental structures in knot theory: the two-component Unlink and the Hopf Link. We lay out a potential use of our work in the domain of plasma physics.

Consider a medium with zero resistivity, where two magnetic field lines are linked together. In such a scenario, these lines will remain linked indefinitely, since magnetic field lines cannot cross or break under ideal conditions. This characteristic makes linked magnetic fields a measure of a physical property known as helicity. In a non-viscous medium, helicity remains conserved over time, as the linked structures cannot change. However, when resistivity is introduced, magnetic field lines tend to reconnect or break, leading to changes in the medium's helicity. The rate of change in helicity becomes proportional to the resistivity of the medium, making helicity a valuable metric for measuring resistivity in such systems.

A tool that can measure the variation in helicity over time would thus be able to quantify the resistivity of the medium. For this, the tool must be capable of distinguishing between a configuration where the magnetic field lines are linked and one where the links have been broken over time. The simplest example of a linked magnetic field structure is the Hopf Link, which consists of two interlinked loops. If this structure breaks apart, it results in two separate, unlinked rings, known as the Unlink. Detecting such a transition is crucial for understanding how helicity evolves in viscous media.

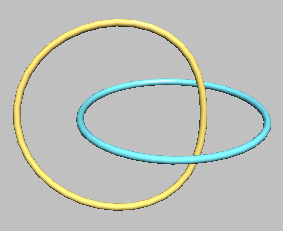
To address this challenge, a computational tool called LINKAGE has been developed. LINKAGE utilizes a topological concept known as the linking number, a numerical value that quantifies the degree of linking between two closed loops in three-dimensional space. By applying Barycentric Equations for Lines and Planes, matrix algebra, and foundational principles of topology, LINKAGE constructs an efficient algorithm capable of calculating the linking number for any given pair of loops. Through this process, subtle differences between the Unlink and the Hopf Link are identified and quantified, much like how DNA fingerprinting distinguishes between individuals based on genetic markers.

At the end, this work includes a dynamic example where multiple interlinked loops were analyzed over different time stamps using the LINKAGE algorithm. By tracking how these links break and evolve, the algorithm showcases its ability to monitor changes in the topological properties of a system. This dynamic analysis underscores the versatility of LINKAGE in studying evolving systems, providing valuable information about the physical processes driving these changes, such as the resistivity of the medium or the rate of magnetic reconnection.