Study of Multiple Interlinked Loops Using LINKAGE

In this section, we extend the study from two component structures to multiple component structures. We explore the potential of such linking number algorithms for studying structures involving multiple interlinked loops. The complex structure we consider is shown in Figure 1 below.

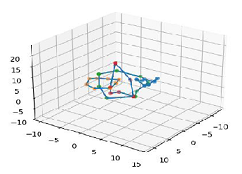
Figure 1: Four loops interlinked with each other.

Figure 2: Removing one loop reduces the number of links from three to one.

The data points have been manually selected to create a structure with four interlinked loops. This example is kept simple for ease of understanding, though the method can be extended to more complex structures with additional loops. We can consider these loops as magnetic field lines evolving over time, with the depicted structure representing one instance in their evolution. At this instance, there are three distinct links present, which we attempt to count using our algorithm. A subroutine within the algorithm calculates the linking number for any given pair of loops. By extending this algorithm to loop over all possible pairs within the structure, we can determine the total number of links at a particular moment. The output is shown below.

# Output Figure 1
The number of links identified is 3

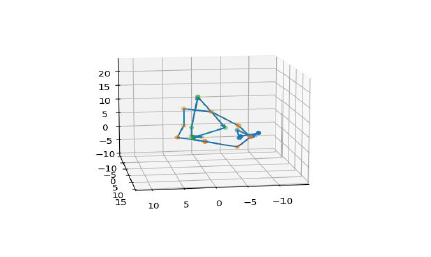
Next, we remove one loop, as shown above, which can be thought of as representing the breaking of magnetic field lines during their evolution. This removal reduces the number of links from three to one, a change accurately captured by the algorithm.

# Output Figure 2
The number of links identified is 1

This approach allows us to track how the number of links in a system changes over time, revealing whether the count increases or decreases at different time instances.