N-Component Helicity Calculation

This Python script calculates the helicity of an n-component link, which is a generalization of the concept of linking number for multiple loops. The code visualizes the loops in 3D, computes the linking number between pairs of loops, and determines whether the structure is a Hopf link. Finally, two structures are compared to check if they are topologically identical.

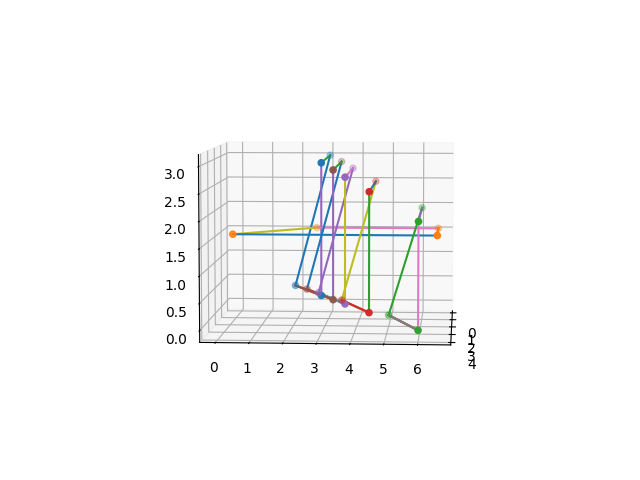
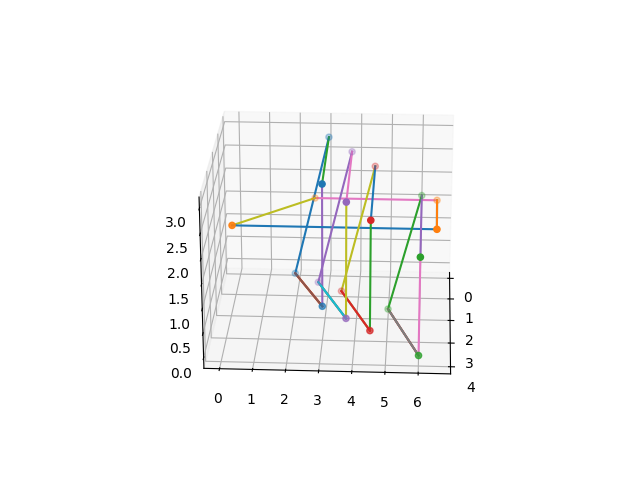
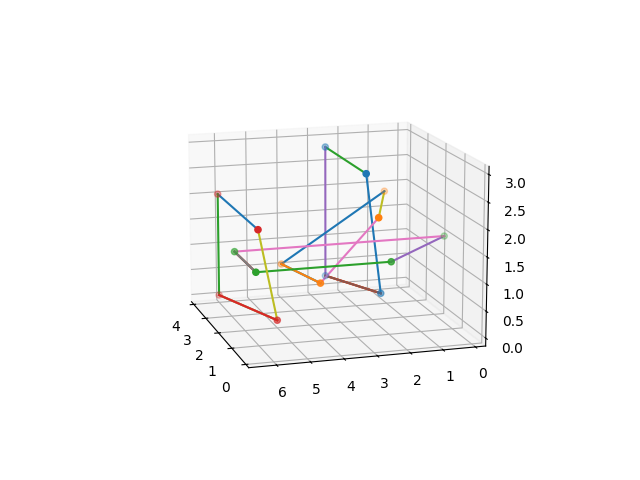
Visualization

The Visualisation() function plots the points and lines that make up each loop in the n-component link. Below is an illustration of the visualized structure:

Linking Number Calculation

The LINKING_NUMBER() function calculates the linking number between two loops. It uses the parametric equations of the loops and solves the equations to find their intersection points. The following steps are involved in the calculation:

Convert the points of the loops to numpy arrays for easier manipulation. Construct triangles from the points of the first loop. Find the parametric equations for the lines of the second loop (red vectors) and for the planes of the triangles (blue triangles). Solve the system of equations to find the intersection points. Determine the orientation of the crossing using the gradient vector and the solution vector.

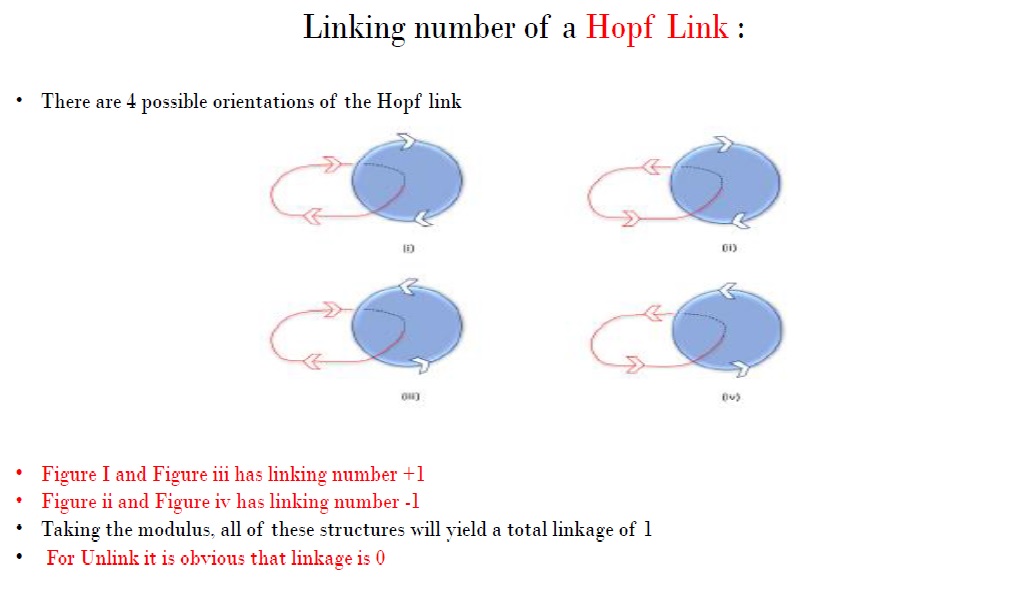
Helicity and Hopf Link Determination

The helicity of the n-component link is calculated by summing the linking numbers for each pair of loops present in the structure, meaning, helicity is the sum of linking numbers for each pair of loops present in the structure. If the helicity matches certain conditions, the structure is determined to be an n-component Hopf link.

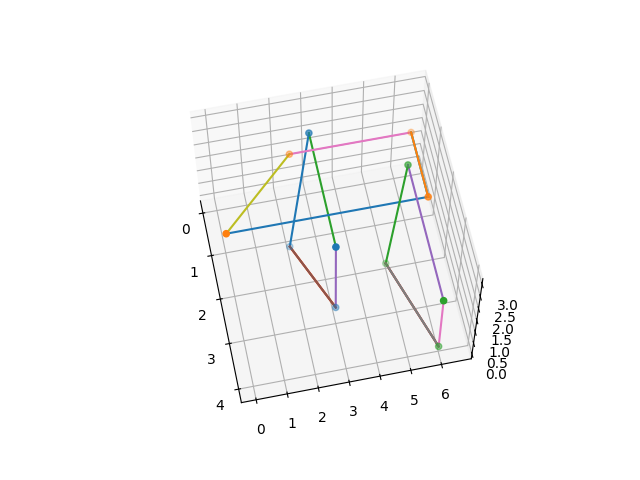
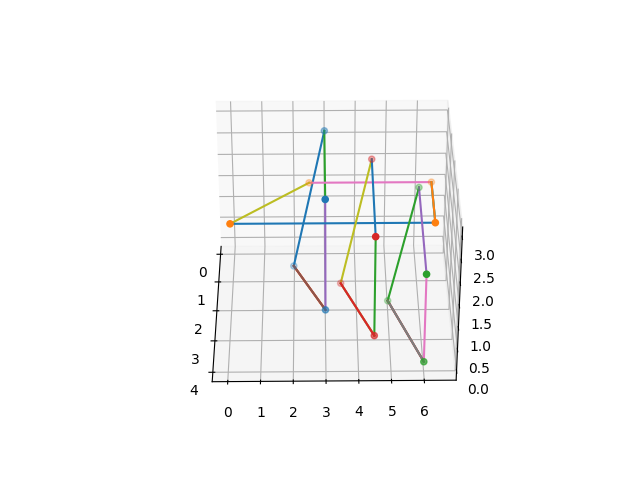
Comparison of Two Structures

The script then compares two structures L1 and L2 to determine if they are the same by calculating their helicity. If the helicity values are equal, the structures are considered topologically identical.