Working Principle

Seifert Surfaces

A German mathematician, Herbert Seifert, provided a valuable algorithm known as Seifert's Algorithm. In this algorithm, he proved that for any knot or link, one can construct an orientable surface with the knot or link as its surface boundary. These surfaces are named after him and are called Seifert Surfaces.

Look at the images shown below. In the first image, there is an orientable surface with the Borromean ring as its boundary. In the second image, there is an orientable surface with the Hopf link as its boundary. In the last image, there are two sides of an orientable disk surface with the unknot as its boundary.

Borromean Seifert Surface
The Seifert surface of the Borromean ring with white and blue representing the two sides of the orientable surface.
Seifert Surface of Hopf Link
The Seifert surface of the Hopf link with two colors showing the orientable surface.
Seifert Surface of Unknot
The Seifert surface of a single unknot, showing both sides of the surface separately.

Connecting the Dots: Linking Number of a Link

Being familiar with the concept of Seifert surfaces, let's attempt to use its feature of orientability to calculate the linking number of a link. Consider a link \(L\) consisting of two knots, \(K1\) and \(K2\).

Link of two oriented trefoils
Link of two oriented trefoils

We select one of the knots, say the red one, and construct its Seifert surface. We then count how many times the blue knot crosses the red Seifert surface. Each time it crosses from the top to the bottom side, we count it as -1; from bottom to top as +1. The modulus of the sum of these values is the linking number of the link.

Linking Number of Unlink

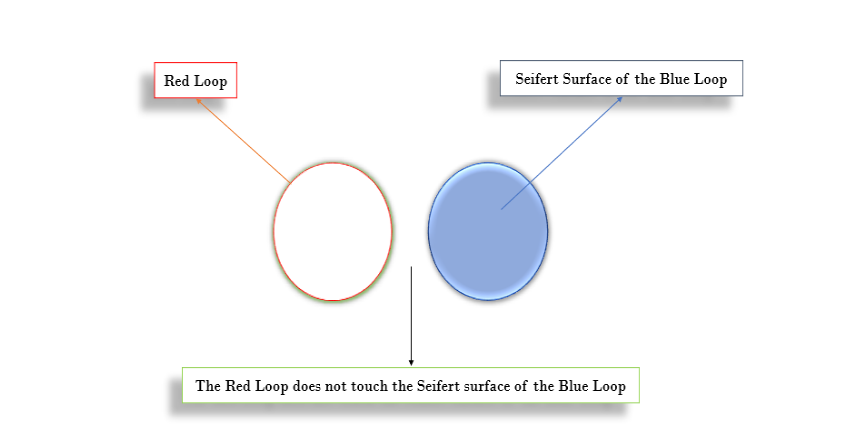
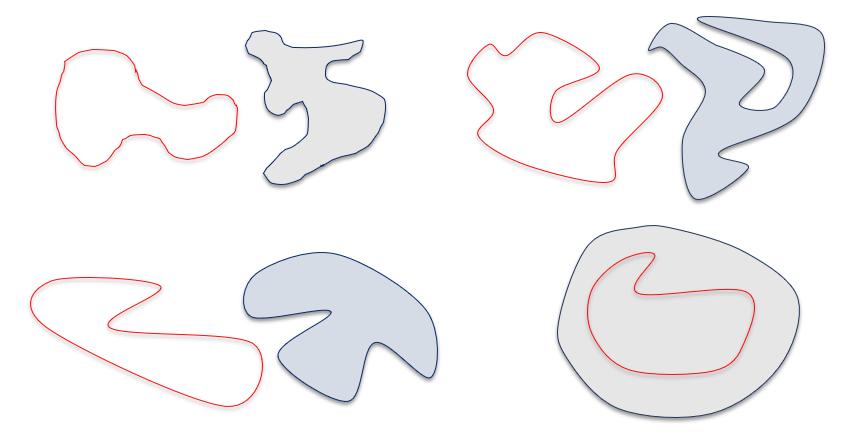
Linking Number 0 for an Unlink
Linking Number 0 for an Unlink
Linking Number 0 for an Unlink
Linking Number 0 for any deformation for an Unlink

The linking number for an unlink is always 0, regardless of the deformations, as the loops do not cross each other’s Seifert surfaces.

Linking Number of Hopf Link

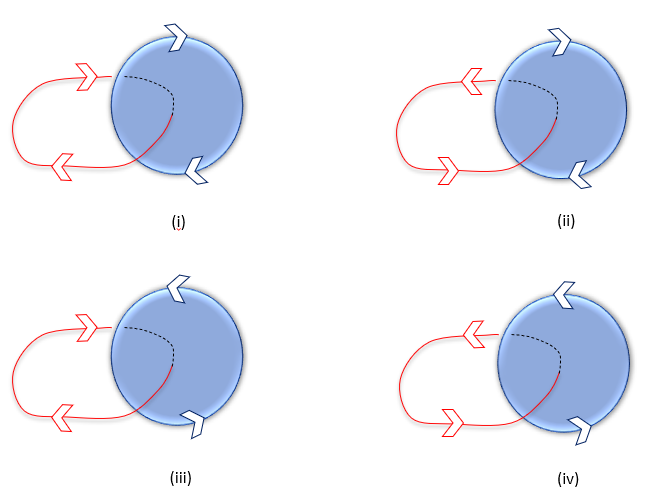
Different Orientations of Hopf Link
Four possible orientations of the Hopf Link

The linking number for the Hopf link is 1, independent of its orientation or deformation, since it crosses the blue seifert surface once, either top to bottom or bottom to top. This distinguishes it topologically from an unlink.