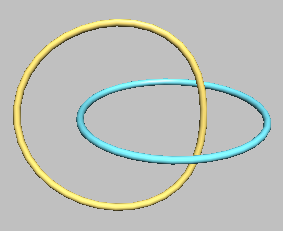A Brief Introduction to Knots and Links

What are Knots? How do they Link?

Let us delve into the intricacies of knots using a simple yet profound example. In the image below, if an ant were to traverse this particular topology, it would perpetually remain entrapped, endlessly looping for the rest of its life. The only way to save the ant from this viscous loop is a decisive cut with a scissor.

This experience prompts us to define a knot as a loop with twists and turns that are impossible to untangle unless cut with a scissor. This holds true for various knots encountered in our daily life. Additionally, there exist simple loops with zero twists and turns, resembling rings of diverse shapes, termed UnKnot from a knot perspective. Also regarded as the trivial knot, it's crucial to note that an Unknot is distinct from a knot and is not a knot.

In mathematics, a knot is an embedding of the circle (S1) into three-dimensional Euclidean space, R3 (also known as E3). Often two knots are considered equivalent if they are ambient isotopic, that is, if there exists a continuous deformation of R3 which takes one knot to the other.

Now, let's elevate the complexity of the problem to the next level. In traditional knots, we had a single strand of rope forming intricate twists and turns, resulting in one-component entities. However, consider a scenario where we have two separate strands, each forming its own loops with twists and turns, and simultaneously intertwining with each other in a complex link that cannot be untangled. These structures are known as two-component links, where two knots are intricately connected. We can further increase the complexity by introducing more components, leading to multiple component links, where several knots interconnect in a sophisticated and inseparable link. The figures below illustrate a few examples of such entities.

Now, within the family of links, we encounter the most straightforward link - the Two-Component Unlink, consisting of two separate unknots. Following the unlink, we have another well-known but more intricate link called the Hopf Link. The Hopf link is composed of two components, both of which are unknots, but in this case, the components are linked together in a single link. The figure below illustrates this example.